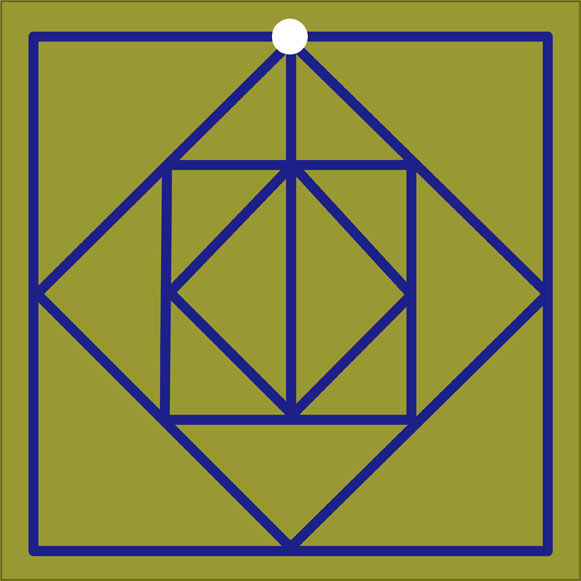
正方形を5個と線分を組み合わせて図形を描きました。この図形は一筆書きをすることができます。もしも、図の上の方に描かれている白丸(始点)から一筆書きを始めるとすると、描き終わり(終点)はどこになるでしょうか。書き終わりの場所を答えて下さい。この図形を一筆書きで描く方法は何通りもありますが、終点は誰が描いても同じ場所になります。
一筆書きができる図形とできない図形
図形を見ると、それが一筆書きができる図形なのかできない図形なのかは、実際に描いて見なくてもわかります。そして、ある条件が整っていれば、始点がわかると終点を答えることができる場合があります。そのことがわかっていれば、一筆書きができない図形に時間を費やすことはなくなります。
下の図形で、Aの方は一筆書きはできませんが、Bの方は一筆書きができます。このことは実際に一筆書きをしてみなくてもわかるのです。一体どのようにしたらわかるのでしょう。AとBの2つの図形を例にして、少しだけ説明しますね。

図形Aについて
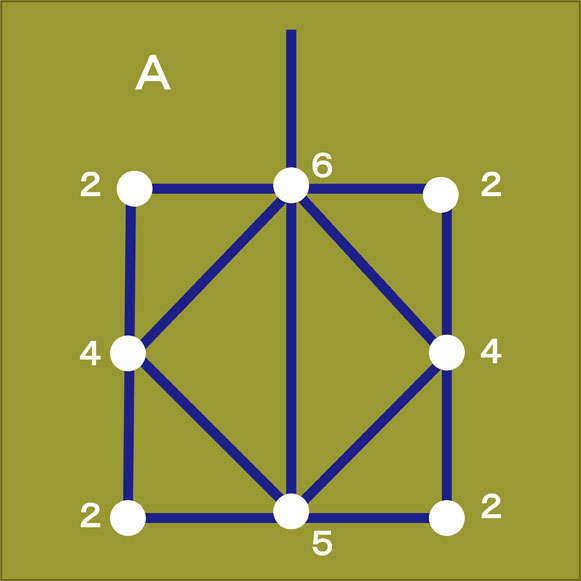
この図形で、白丸から何本の線が出ているかを記入してみました。この図形で使われている線はまっすぐですが、一筆書きで使われる線は曲線でも構いません。
白丸から偶数本の線が出ている点が7個あります。このような点を偶数点(偶点)といいます。白丸から奇数本の線が出ている点が1個あります。このような点を奇数点(奇点)といいます。つまり、図形Aには偶数点が7個、奇数点が1個あるということがわかります。では、図形Bはどうでしょうか。
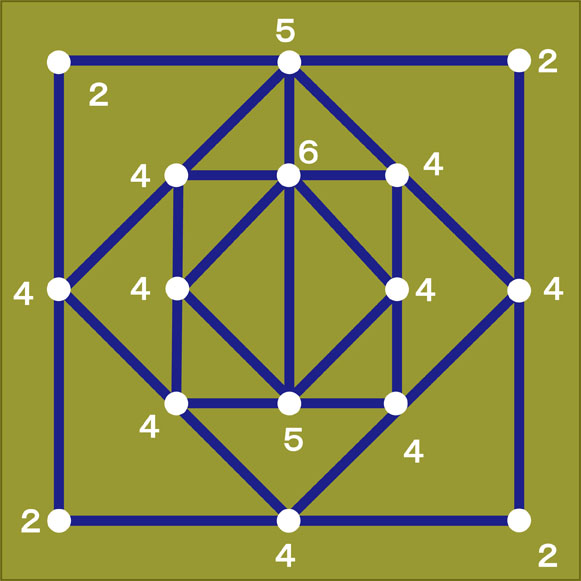
図形Bについて
図形Bには、偶数点が6個、奇数点が2個あります。

偶数点と奇数点の数でわかること。
一筆書きができる図形は、奇数点がないか、または奇数点が2個だけある場合です。奇数点が2個ある場合、どちらかの奇数点が始点で、もう一方の奇数点が終点となるということがわかっています。
奇数点がないということは、すべての点が偶数点ということになります。つまり、すべての点が通過点ですから、どの点から描き始めても一筆書きをすることができて、始点と終点は一致します。

もとの図形の偶数点と奇数点を確認してみましょう。
奇数点が2個ですから、この図形は一筆書きができることは間違いありません。始点は指定されていましたから、終点として考えられる場所は1か所だけです。さて、それはどこでしょうか。
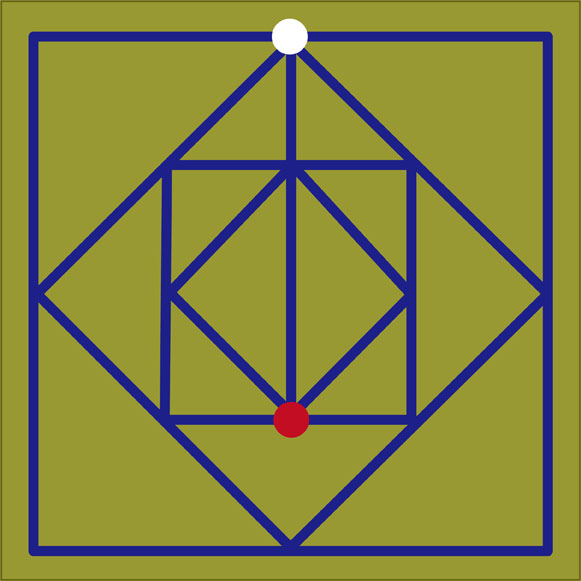
答えです。
始点として指定されていたのは奇数点である白丸の場所でした。つまり、終点は、もう1か所の奇数点である赤丸の場所です。
偶数点や奇数点の個数を調べると、一筆書きができるかどうかがわかったり、始点や終点の場所がわかったりします。しかし、一筆書きの方法自体は一通りではありません。それは描く人によって同じだったり異なっていたりします。色々と試して見て下さい。
実際に描いて見なくても、一筆書きができるかできないかはすぐにわかるんですね。でも、実際に描いてみるのも楽しいものです。一筆書きの問題には、瞬時に判れば天才!一筆書きの終点を答えよ! という問題もありました。


